Wednesday, March 02, 2011
Using Iridium Flares for Parallax Measurements (part 2)
 Overlay of two separate flares simultaneously at a) Largs North, SA and b) Blackwood SA, images overlaid using The GIMP. My image was taken with a Canon IXUS, 400 ASA, 15 second exposure. You may need to click on the image to embiggen and see the reference stars.
Overlay of two separate flares simultaneously at a) Largs North, SA and b) Blackwood SA, images overlaid using The GIMP. My image was taken with a Canon IXUS, 400 ASA, 15 second exposure. You may need to click on the image to embiggen and see the reference stars. Back in October I posted about an Iridium flare captured by Dean Male and myself. From those images I tried to calculate the height of the Iridium satellite using parallax. The figure came out too high, but not too bad for measurements done with pencil marks on a bit of paper.
So we decided to try again. After a couple of false starts (curse you weather) Dean and I finally got another good shot of an iridium flare last night (March 1).It helped that from my vantage point, it was a -8 magnitude flare, which was stunning, the brightest flare I've even seen (Dean only saw magnitude -3, to put this in perspective, Venus is magnitude -4)
As for last time, I measured the distance between the two flares and reference stars (6, 9 and 12 Hydrae respectively). I measured the distances using ImageJ (and calibrating the scale of the images against the known angular separations of 6, 9 and 12 Hydrae). This is a bit more accurate than the pencil mark on paper. As before, I used the formula used for Lunar parallax:
Knowing that Dean and I were 12.5 Km apart, I calculated a distance of 961 Km, it should be 801 Km (Iridium 65 was 791 km vertically above the earth, but as it was offset from us, the actual path length is longer).
So, better than the first attempt, but still well outside the 3% error achieved for measuring the distance of the Moon using simple photography. I've been racking my brains as to why I'm not getting better accuracy. The only things I can think of are:
1) Dean and I aren't really 12.5 Km apart but are something more like 10.5 due to triangulation effects (but, I can't make the maths work with the Cal Sky data)
2) The fact that we are measuring the flares a substantial distance below the zenith, which might mess up the assumptions for the equation but I still think the effect would be small.
3) Altitude, I'm at sea level, Dean is up higher (nah, that night compensate for being below the Zenith).
I'm stumped at the moment. Any ideas?
UPDATE: Having thought about the geometry for a while, I realised I was measuring the distance angle perpendicular to the flare, instead of North-South (or East -West), so the measured angle didn't correspond to the geometry of the viewing.
When I did this, I got 787 Km, which is within 1.8% of the actual distance (801 Km).
So YAAYYYY!!! I spent a lot of time trying to work out how to visualise the angles to draw a diagram of the situation, and this made me realise I was using the wrong measurements.
Labels: gimp, imageJ, iridium flares, Satellite
I've been doing other circular stuff for lightning protection recently, but not enough to get a grip on the parallax problem.
Well done Ian !
<< Home
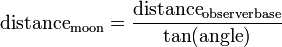




 Click to read about or order
Click to read about or order Click to read about or order
Click to read about or order Click to read about or order
Click to read about or order Click to read about or order
Click to read about or order




